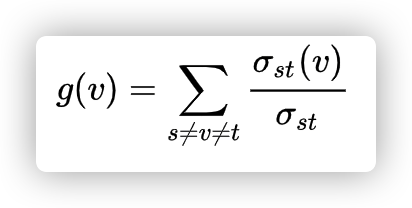图计算之BetweennessCentrality算法

2022-02-12

图

之前已经了解了 Rank 类的算法, 三角计数/聚集系数, 今天来看看中心性类的算法代表 —- 中介中心性算法是如何在 hugegraph 的图计算系统中实现的.

0x00. 前言

关于中心性算法的分类可以参考之前提过的 Neo4j 的算法书籍, 以及 TigerGraph 的算法文档页面, 简单来说, 中心性算法就是计算每个点在图中的一个影响因子, 这个影响内容可以是紧密性, 也可以是重要性/受欢迎度等, 也可以是其他类似的定义, 这里主要是

1. 中心性

简单看看介绍即可, 它有常见的几种, 度中心性相对简单, 中介相对复杂

中心性是用来衡量一个节点在整个网络图中所在中心程度的概念，包括度中心性、接近中心性、中介中心性等。其中度中心性通过节点的度数（即关联的边数）来刻画节点的受欢迎程度，接近中心性是通过计算每个节点到全图其他所有节点的路径和来刻画节点与其他所有节点的关系密切程度

2. 逻辑定义

首先中介性是说算图中每个点出现在其它任意两个顶点间最短路径的次数, 从而找出对子图之间起到重要桥梁的点, 最后某个点 V 的中介值是由 “V 出现在两点最短路径数 / 两点总最短路径数” 的比值累加. 孤点不参与计算, 中介值为 0, 简单例子:

A 和 E 点之间有三条最短路径, 分别是 A->B->E, A->C->E, A->D->E
那么 A->E 对 B 点的中介 vote 就是 1/3
依此累加全图中任两点间的 vote 给 B, 就是 B 的最终中介系数值.

那么容易推算到全图中(非相邻)两点的最短路径计算 + 存储, 会是一个很大的时空占用, 所以一般会设定一个采样系数(sample), 比如 V 有 10 条出边, 采样率为 1 代表全部遍历, 采样率 0.5 则代表随机挑选其中一半的边遍历, 从而优化性能.

最后, 因为最短路径本身分为带权/无权查找, 也就导致在中介性里也会对应不同的实现(BFS or Dijkstra), 也可看出中介性也是强依赖于最短路径作为基础的.

注:

最短路径这里定义是不相邻的两点, 如A->B->C, A 和 B 相邻则不计算最短路径
V 在两点最短路径经过的次数, 其中首/尾(起始/终点)是不计算的, 例如 A->B->C->E, 只有 B 和 C 是经过点
无向图而言, 两点A 和 C 的最短路径应该只计算一次 vote, 也就是说 A 给 B 投票了, C 就不应重投 (或结果除以2). 有向图不需单独处理.

3. 具体定义

从上面逻辑的理解里其实已经看出它的计算公式了, 参考 wikipedia:

其中 v 代表当前点, s ≠ v ≠ t 就是上面备注中说的, 计算路径是不包括起点/终点的, st 就代表任意两点的最短路径.

4. 使用场景

金融风控领域中反欺诈场景里中介实体的识别

安全领域查找黑产团伙的中间商

医药领域中特定疾病控制基因的识别，用以改进药品的靶点 (?)

0x01. 举例

中介中心性的描述稍复杂一点, 一般都会以具体的例子来熟悉它, 引用里基本都有例子, 这里简单举例一个:

graph LR
v0-->v1-->v2-->v3
v0-->v2

假设上面是有向图, 双向边, 也就是互相关联, 那么上图中0, 1, 3的中介性都是0, 2的中介系数是4, 由 0 到 3 + 1 到 3贡献:

0–>2–>3 (总共1条最短路径, 2 获得 v1 vote 的全部权重)
1–>2–>3 (同上)

然后以 3 为起点, 到 0 和 1, 也有相反的两条路径, 所以 3 会给 2 贡献两次 vote, 总和为4 (如果这是无向图, 结果除2去重即可)

0x02. 实现

理解了中介中心性的定义和场景之后, 再回到 pregel 的模型中, 因为它限制了每一轮有且只能走 1 步, 所以就需要在每一次迭代计算中携带自己存储的路径信息, 以及接收的 vote 信息, 并传递给它的所有出边, 那关键点是求出两点间的所有最短路径 (all shortest path)

这是论文里的实现步骤:

然后看看代码里的具体实现:

在 SS0, 做两个事:
- 排除孤立点, 没有出边的点直接跳过不会参与后续任何计算
- 非孤点初始化自己的中介值为0, 以及一个 path-list, 并发送给所有出边
正式的计算中, 分为两个主部分:
- 迭代当前点收到的消息 (入边发来), 判断是否需要累加中介值, 以及是否需要把消息更新路径后, 转发给自己的出边
- 清空当前轮存储的映射信息, 判断当前点是否给目标点vote, 或是走到最大遍历深度, 则标记 inactive 退出.

先看看 SS0 的过程:

@Override
public void compute0(ComputationContext context, Vertex vertex) {
    // First superstep is special, we just send vertex id to its neighbors
    BetweennessValue initialValue = new BetweennessValue(0.0D);
    initialValue.arrivedVertices().add(vertex.id());
    vertex.value(initialValue);
    if (vertex.numEdges() == 0) {
        return;
    }

    IdList sequence = new IdList();
    sequence.add(vertex.id());
    context.sendMessageToAllEdges(vertex, new BetweennessMessage(sequence));
    LOG.info("Finished compute-0 step {} {}", vertex.id(), vertex.numEdges());
}

再看看第二轮开始:

public void compute(ComputationContext context, Vertex vertex,
                    Iterator<BetweennessMessage> messages) {
    BetweennessValue value = vertex.value();
    // The betweenness value to be updated
    DoubleValue betweenness = value.betweenness();
    // Collect the vertices sent here this time
    IdSet arrivingVertices = new IdSet();
    while (messages.hasNext()) {
        BetweennessMessage message = messages.next();
        // The value contributed to the intermediate node on the path
        DoubleValue vote = message.vote();
        betweenness.value(betweenness.value() + vote.value());

        this.forward(context, vertex, message.sequence(), arrivingVertices);
    }
    value.arrivedVertices().addAll(arrivingVertices);

    boolean active = !this.seqTable.isEmpty();
    if (active) {
        this.voteThenSendMsg(context);
        // TODO: test perf
        this.seqTable = new HashMap<>();
        //this.seqTable.clear();
    } else {
        vertex.inactivate();
    }
}

private void forward(ComputationContext context, Vertex vertex,
                     IdList sequence, IdSet arrivingVertices) {
    if (sequence.size() == 0) {
        return;
    }

    BetweennessValue value = vertex.value();
    IdSet arrivedVertices = value.arrivedVertices();
    Id source = sequence.get(0);

    // The source vertex is arriving at first time
    if (arrivedVertices.size() < this.storePerf &&
        !arrivedVertices.contains(source)) {
        arrivingVertices.add(source);

        SeqCount seqCount = this.seqTable.computeIfAbsent(
                            source, k -> new SeqCount());
        seqCount.totalCount++;
        // Accumulate the number of shortest paths for intermediate vertices
        for (int i = 1; i < sequence.size(); i++) {
            Id id = sequence.get(i);
            Map<Id, Integer> idCount = seqCount.idCount;
            idCount.put(id, idCount.getOrDefault(id, 0) + 1);
        }

        Id selfId = vertex.id();
        sequence.add(selfId);
        BetweennessMessage newMessage = new BetweennessMessage(sequence);
        for (Edge edge : vertex.edges()) {
            Id targetId = edge.targetId();
            if (this.sample(selfId, targetId, edge) &&
                !sequence.contains(targetId)) {
                context.sendMessage(targetId, newMessage);
            }
        }
    }
}

private void voteThenSendMsg(ComputationContext context) {
    for (SeqCount seqCount : this.seqTable.values()) {
        for (Map.Entry<Id, Integer> entry : seqCount.idCount.entrySet()) {
            double vote = (double) entry.getValue() / seqCount.totalCount;
            BetweennessMessage voteMessage = new BetweennessMessage(
                                             new DoubleValue(vote));

            context.sendMessage(entry.getKey(), voteMessage);
        }
    }
}

0x03. 启动方式

同样以 k8s 提交任务来举例, 除了配置可调整的参数外, 启动和销毁方式都挺简单, 以推特2010数据集为例:

apiVersion: hugegraph.baidu.com/v1
kind: HugeGraphComputerJob
metadata:
  namespace: hugegraph-computer-system
  name: &jobName bet-hdfs
spec:
  jobId: *jobName
  algorithmName: bet-twitter
  image: imbajin/xxx-algorithm:1.0.0 # test image (or use official version)
  pullPolicy: Always
  workerInstances: 30
  workerCpu: "5"
  workerMemory: "12Gi"
  configMapPaths:
    hdfs-conf: /opt/hdfs_conf
    #stanford-loader-config: /opt/dataset # 斯坦福数据集, 需先挂载
    twitter-loader-config: /opt/dataset # 推特数据集存于hdfs, 需先挂载
  computerConf:
    job.partitions_count: "120" # 分区数, 结合节点和负载情况分配
    job.partitions_thread_nums: "4" # 并行度
    betweenness_centrality.sample_rate: "0.001"
    bsp.max_super_step: "5"
    algorithm.params_class: com.baidu.hugegraph.computer.algorithm.centrality.betweenness.BetweennessCentralityParams
    input.source_type: "hugegraph-loader"
    input.loader_struct_path: "/opt/dataset/struct.json"
    input.loader_schema_path: "/opt/dataset/schema.json"

待 wiki 转过来

0x04. 优化点

中介性算法计算过程的理解并不复杂, 但是麻烦的是具体的实现方式, 如何记录全部最短路径, 以及各种情况的判断和去重, 大概有这几点关键点:

每个点存储路径压缩
控制传播消息量
sample 算法

这里还有不少性能优化的事项, 就单独拆分为一个图计算的性能优化文档了.

其他详见源码

参考资料: