VectorDB 目前成为了 LLM 的上下文之基础设施部分, 一起来了解认识它, 因为内容的确是有些多, 上下文掺杂起来需要分多次梳理
[TOC]
0x00. 前言
VectorDB 作为一个比较特殊的细分领域的数据库, 其实诞生时间是远早于 LLM/GPT 到来的时间的, 最早它被用来做各种”以图搜图“/“听歌识曲“等相似度功能而作为一个不少炼金术士知晓, 但是并不熟为人知的存在, 随着 LLM/GPT 的划时代出现, 突然变成市场上最热的一颗星.
这里补充一些基本的知识, 帮我们更好的理解后续的上下文, 否则会有许多似是而非的地方
奇怪的数字?
初识 AI/LLM 的同学可能会经常感到困惑, 比如需要通过各种方式把文本/图案/音视频先都转换为一个奇怪的浮点数/整数, 有些还带有正负号, 不太明白为何不能直接解析字符串之类的, 这是由于大部分 LLM 背后是”神经网络“模型, 基本只适合处理数值类型, 并且:
- 字符/图像/音视频世界非常复杂, 语义是不方便计算机直接理解的
- 而数字类型背后则是数学体系, 通常有严密和推导的运算规则, 也更容易被计算机高效存储/压缩/矩阵运算等
另外, 绝大部分的 LLM(包括 GPT) 目前也并不是真正理解文本的语义和语境, 它本质是通过大量的训练数据来学习文本中隐含的统计规律和概率分布, 从而生成/预测下一个最可能的单词或句子, 简而言之, LLM 目前主要是根据已有素材来进行”更好的模仿“
Token 的由来
token 这个词常见于 GPT 的参数返回里我们可看到 cost: 5 token这样的字样, 以为它是一个 cost 的计量单位, 实际它是分词器的最小表示单位:
GPT*使用了一个特定的 BPE 分词器(tokenizer)来将文本切分成多个 token, 不同分词器会得到不同的 token- 接着将每个 token 转换成一个数字编码, GPT* 模型只能理解这些数字编码(
31414), 而不能直接理解原始的文本(hello) - 然后将这些数字编码输入到一个多层的 Transformer 解码器中捕捉 token 之间的关系和依赖, 从而生成下一个最可能的数字编码
- 最后再将这个数字编码转换回对应的文本 token 返回给用户, 从而让你看起来感觉像是完成了
“文本理解” + “文本生成“ - OpenAPI 表示 一般 1 token ≈ 4 字节字符串(不固定),
hello就会转为 1 个 token,hello?则会是两个, 也取决于分词器的切分
这个比例并不是固定的,因为不同的字符序列可能被切分成不同数量的token。例如,“hello”这个单词被切分成一个token,而“hello!”这个单词加上感叹号被切分成两个 token (取决于分词器的实现)
如果输入或输出的文本超过了token限制,那么 GPT*模型会截断超出部分,并只处理截断后的文本。(这就类似”脑袋不够用了, 清空一下”..)
LLM 本身不提供”记忆”
这里有一个常被误解的两个误区, 一个是以为 LLM/ChatGPT 本身有上下文记忆功能, 你跟它多次对话的时候有一个更真实的环境, 其实不然:
- 简单来说, 这个对话记录是被存储到了 “内存“/“数据库“中
*ChatGPT会被设定为, 你每次发送新的”消息”给它, 则它从缓存中读出之前的内容, 然后帮你自动”拼接 + 揉和”成了新的段落重新去整段提问- 例如你分别给
*GPT打了三句话 “hello“, “how are u?“, “I’m Tom“, GPT 在你输入每句话后, 都会遵循token 化的过程处理返回你新的答案 - 但是对它来说, 后续的对话, 则会自动把之前的输入 + 输出都揉入进去, 从而给你一种它是有”记忆“的错觉了
- 例如你分别给
- 所以越大的输入输出, 就会带来越为沉重的 token 成本/性能问题 (例如我直接上传一个几百 MB 的文档, 那就直接
OOM了)
于是, 向量数据库就作为一个解决 LLM 局限性的方案之一, 它核心功能也是把文本/音视频转为向量存储, 然后把提问转换为”搜索相似度最高的向量/context”, 核心理念和 GPT 的方案其实本质相近, 那它的优势在哪呢?
VectorDB 的角色
最典型的例子, 就是上面说的一个巨大的文本/书籍, 甚至以后的音视频等”大块头“, 把这么大的输入直接放 LLM/GPT 的内存中去耗费它的计算资源是不适合的, 利用 VectorDB 后的步骤是:
- 把大文本 –转换–> 为向量 (vector-embedding), 比如用户上传的几百MB 的文件, 就可以转换后丢进来
- 用户提问”上传文档中的第三章主要讲的什么?” –> 把提问转换为向量, 然后调用相似度匹配算法找出多个接近”context“
- 把 “context” 返回给 GPT, 然后再把这个作为 GPT 的输入进行正式问答, 从而大幅减少了 GPT 自身的计算量 (实现类似”计算下推”的效果)
那你可能会说, 这个场景似乎也比较局限, 其他的通用对话里能应用么? 其实也可以, 例如你和 GPT 有了多轮长对话, 则可以把所有对话文本都转向量存储起来, 然后接着再提问的时候, 将新的问题文本向量化后, 和之前的记录做相关度搜索, 找出需要的”增量上文“, 再发送给 GPT, 而不是一股脑把所有的”全量上文“ 揉合后发给它, 自然也是达到了大幅”降本增效”的作用.
什么是特征工程/向量化?
上面有个关键概念是 XX 的向量化(vector-embedding), 那么我们自然会有个疑问, 这里的向量具体是啥怎么存储, 怎么搜索的, 这里简单来说一下, 先回想传统 DB 的精准搜索, 这个我们容易理解, 它的索引通常是一颗树, 通过”前缀匹配/二分查找“为常见方式进行”精准“匹配, 但它对”语义搜索”就支持的很弱, 那这里的”语义“具体是指的什么呢?
比如最典型的搜索是字母顺序二分, 比如你搜索”苹果“, 它就只会出现它精准匹配后的 *苹果*的语义, 而不会联想到梨子, 也不会联想到 Android, 在之前需要人工来把 “苹果” 和 “梨子” 和”Android/手机”等词汇进行打标签关联, 生成 + 选特征的过程, 就被称为 Feature Engineering (特征工程)
文本的标注还算比较容易(特征维度较少), 到了图片/音视频的时代, 一张图片有非常多纬度的特征(颜色/大小/RGB/分辨率/纹理…), 人为标注基本很难完成, 这个时候自动进行特征工程的向量化就出现了, 它通常由 AI/LLM 模型提供一套/多套转换算法, 类似 text2vec/pic2vec/ voice2vec / vedio2vec 等, 来自动的根据这些数据的通用特点加以转换和标注, 例如下面是 OpenAPI 提供的文本转换例子: (清晰的输入 + 输出)
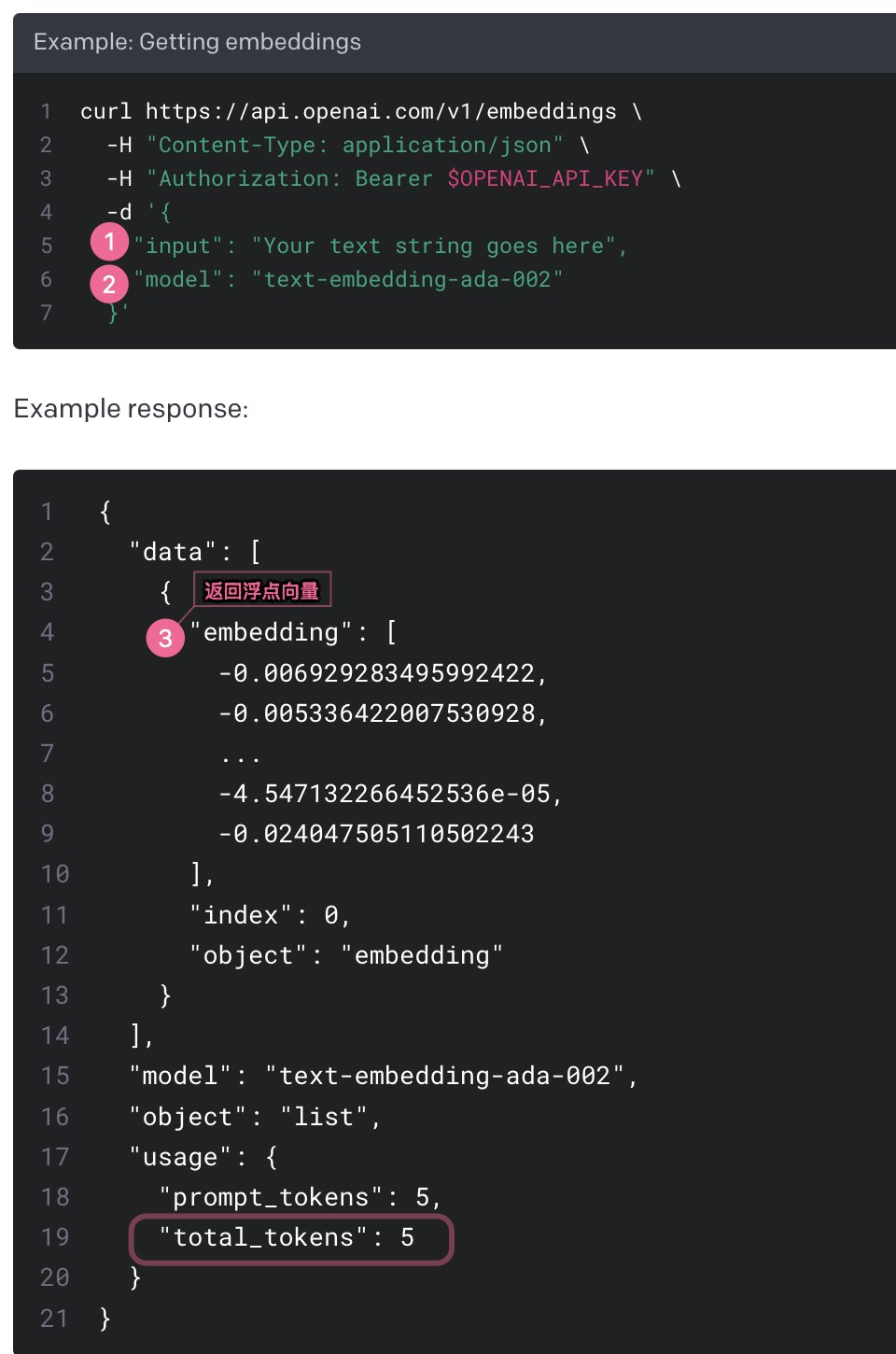
那么这里 embedding 数组的长度, 也就是向量的”维度“, 可以看到一行简短的文本字符串, 对应就有多达 1500 维之多, 由此可见它的存储/计算就必然是有许多值得探索/优化的地方的, 否则存储开销都会相当感人.
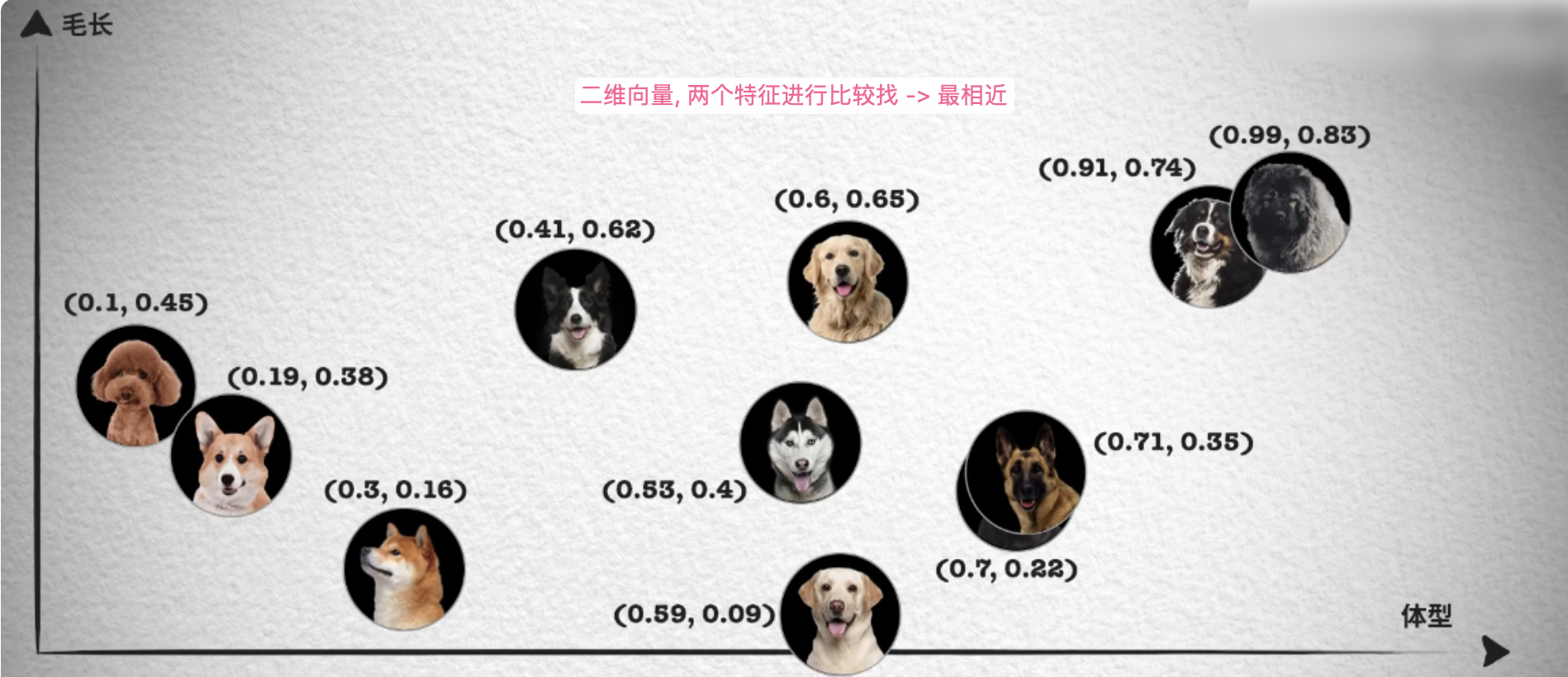
你可能会很奇怪不知道为何一行简单的文本需要生成这么多维的向量, 也不知道对应的数值含义, 那下面这个经典的图片特征抽取就很容易理解了, 首先是单一维度(一维向量), 我们要分辨不同的 🐶 狗, 可以简单的对它们的体型打分 (0~1)排序, 然后得到下面的例子:
然后你会发现如果我传入一个体型分数 0.56, 它就会在几个不同类型的狗之间产生冲突不知道哪个是最贴近的, 直观来说, 我们就可以新增另一个维度的特征来进行分辨, 比如说是长/短毛, 然后类似的我们在这个维度上按 0~1 也进行打分, 就得到了一个 X-Y 轴的二维向量:
依次类推, 只要特征足够的多, 那么找出上千个可区分的方式进行特征打分, 得到一个N 维向量, 而向量是具有
“大小 +方向”的数学结构, 转换后就能通过计算向量之间的距离来判断它们的相似度, 这就是相似性搜索 . 例如此时用户随意输入一张小狗照片, 也就能最快找到与之相似的 TopN 图片了, 这也就是”以图搜图/听歌识曲“的基本原理
至于具体如何去进行向量化的,
目前常见有 3 类向量化(embedding)的方式:
- 矩阵分解法:
SVD,LSA(将高维矩阵映射成两个低维矩阵的乘积) - 基于自然语言处理(NLP):
word2vec,FastText(将每个单词/短语映射到一个低维向量空间中) - 基于图(Graph):
deepwalk,node2vec,metapath2vec(把图中的点以低维稠密向量的形式进行表达)
此部分非关注重点, 仅简单列举, 不深究细节..
0x01. LLM 当前的缺陷
通过前述可以知道, 目前 LLM 主要有几个问题:
- 上下文限制
- 性能问题
- ==幻觉 (编造) /SEC==
- 可解释性
粗略的看, 其中 ①② 是可以用向量数据库来改善的, ③④ 则是可以用 KG 来改善的, 当然实际也可以有交叉, 之后可以尝试看看
- 输入长度/大小的限制 (token limitation), 例如
GPT-3.5-Turbo下默认可能限 3k 字,GPT-4则限制 30k 字 - 长对话/大文本输入的计算开销
- 基于准确参考信息的模拟, 可以大幅降低幻觉/SEC 问题 (RAG 天然抑制)
- 对用户来说更加透明 (好比搜索引擎可引用资料, 易溯源, 降低黑盒比例)
0x02. 向量距离
常见:
欧式距离 (Euclidean, 简称 L2)
内积 (inner-product, 缩写 IP)
余弦相似度 (Cosin)
汉明距离 (Hamming)
杰卡德 (Jaccard)
0x03. 相似性搜索
前言中提到了向量搜索本质就是相似性搜索 (Similarity Search), 也就是寻找多维空间里向量距离最近的 TopN, 可是我们很容易想到, 哪怕是有了不同类型下的距离计算方式, 最原始的方式仍是某个输入向量, 需要和整个库里的所有已有向量进行挨个比较/计算, 也就是 O(n) 的时间开销, 而且维度越大, 计算开销越大, 几乎不可接受
所以我们需要高效的方式来避免暴力搜索向量距离最近的 TopN:
- 向量降维/精简
- 缩小搜索范围 (limit range)
- 聚类算法:
K-Means, Faiss 中引入的算法等 - 乘积量化: PQ
- 树/图结构化: HNSW
- Hash 分组
- 聚类算法:
另外, 2 中寻找最接近向量的过程, 有一个专有名词 ANN(Approximate Nearest Neighbor) 来表示, 是一个汇总各类算法/数据结构找邻居的说法
A. 向量降维
很好理解, 过多的维度里一般会有一些类似/冗余的维度, 为了节省存储成本和计算量, 我们就可以提取相似的特征进行压缩/合并, 常见的方式
PCA(主成分分析):一种线性降维方法,通过找到最大化数据方差的正交投影方向,将高维数据投影到低维子空间中,从而保留数据的主要特征和变化趋势。PCA 可以用于图像压缩、人脸识别、特征提取等场景。
LDA(线性判别分析):一种监督学习的线性降维方法,通过找到最大化类间距离和最小化类内距离的投影方向,将高维数据投影到低维子空间中,从而提高数据的分类性能。LDA 可以用于人脸识别、文本分类、情感分析等场景。
MDS(多维尺度变换):一种非线性降维方法,通过保持原始空间中样本之间的距离在低维空间中不变或近似不变,将高维数据映射到低维空间中。MDS 可以用于社交网络分析、品牌定位、心理学研究等场景。
ISOMAP(等距特征映射):一种非线性降维方法,通过构建邻域图并计算样本之间的测地距离(即沿着流形表面的最短路径),然后使用 MDS 方法将高维数据映射到低维空间中。ISOMAP 可以用于图像处理、语音识别、生物信息学等场景。
SNE(随机邻域嵌入):一种非线性降维方法,通过使用概率分布来描述样本之间的相似度,并最小化原始空间和低维空间中相似度分布之间的差异,将高维数据映射到低维空间中。SNE 可以用于可视化高维数据、探索数据结构等场景。
T-SNE(t-分布随机邻域嵌入):一种改进的 SNE 方法,通过使用 t-分布来替代原来的高斯分布来描述低维空间中样本之间的相似度,并采用梯度下降法来优化目标函数,将高维数据映射到低维空间中。T-SNE 可以用于可视化高维数据、探索数据结构等场景。
Refer: 六种常见数据降维方法简介及代码实现 - Zhihu
之所以降到低维度并不是默认做法或者最佳实践思路, 主要有几点影响:
- 降维可能带来”失真“, 降低数据区分度和准确性
- 线性降维方法可能无法处理非线性数据,而非线性降维方法可能无法保证全局最优(贪心)
- 压缩/降维本身的计算开销也会增加
此部分非本篇核心, 可自行查阅相关资料, 此处暂略
B. 缩小范围
在缩小范围的常见方法之前, 我们首先介绍一下最原始的枚举版本 Flat, 它经常与其他向量索引一起出现, 实际主要是用作一个”对比/参照”
Flat
与之前的索引不同, Flat 不是一个缩写, 它就是”平面的”意思, 索引方式也最为简单, 引入一个新的辅助查询向量(query vector) xq , 然后暴力的将所有存储的向量与之进行距离计算(穷举), 计算完成后反馈 TopK 距离的向量, 能达到 100% 的召回率, 但显然拥有最慢的查询速度和普通的内存开销.
所以一般来说, 除了极小的数据集, 一般很少有生产环境直接使用 Flat 的存在, 它更多可以作为一个对比参照组
然后, 就进入正式的”缩小范围”方式介绍, 首先从聚类开始说起, 它简单说就是”分类/分组“的意思, 把存储后的向量再做一个区域划分, 它与”图”中的”社群发现“本质是一类, 可以理解为是一种限于 Graph 中的”图聚类”, 聚类中的”距离判断”变为了”中介度/中心性”判断, 再直接点说类似分库分表, 对数据进行一次预处理, 从而减少搜索范围
K-Means (聚类索引)
这是一个很经典的划分算法, 在后面的向量索引中你会经常看到应用到这个算法,
- 设定初始值, 最重要的是 K 个分类 (固定), 然后(默认)随机取一个中心点 (又称为”聚类中心”)
- 把每个(向量)点分配到离它最近的聚类中心 K
n上 (一般用欧式距离) - 计算每个聚类(社群)的新中心 (取每个维度上的平均值, 例如 m 维向量的中心可取社群所有向量每个维度平均值)
- 重复 step 2~3, 直至中心点不再改变 or 到达最大迭代次数
划分后再搜索时, 就先判断当前向量属于那个簇( 群组), 从而根据 K 的个数只需要最少 1/K 的搜索范围了, 最好的情况它期望簇之间的距离尽可能大, 簇内向量元素则尽可能小, 这样区分度就会高 (反之则效果减弱)
缺点:
- 分类不均/不突出时, 搜索准确性会降低 (例如待查向量处在两个簇中间)
- 简单直接, 但高维/大数据向量计算慢
IVF (倒排索引)
IVF(Inverted File)
LSH (哈希索引)
LSH(Locality Sensitive Hashing)从名字就能知道核心是 Hash 的思想, 也就继承了 Hash 的核心特性, 用空间换时间, 追求 O(1) 的查找速度, 那接下来就要思考几个关键点: 多维向量是如何进行 hash 分桶, 又是如何解决冲突以及查找的问题的
首先, LSH 不同于传统精准查找, 它追求的是最大化 hash 冲突的(而不是尽量避免冲突), 这是为何呢? 因为 hash 冲突也就意味着”相同/相似“, 本来 ANN 就是寻找相似的 TopN, 而不是找一个唯一/精准值, 所以 LSH 尽可能让类似的元素分到一个桶里, 这样更快找到相似的一堆值, 由此它就需要专门设计的一套 hash 算法, 使得向量距离越近的元素映射到一个桶里 (其实本质来说它也算是一种聚类)
LSH 转换后得到的是一堆二进制的数值, 所以它比较距离的时候一般是使用汉明距离, 通过统计二进制的不同位数来寻找相似性.
为了方便理解, 还是举个具体例子, 假设我们有以下四个文本:
- A: “我喜欢吃苹果”
- B: “我喜欢吃香蕉”
- C: “我喜欢吃橘子”
- D: “我不喜欢吃水果”
我们想要比较这四个文本之间的相似度,并找出与给定文本最相似的文本。我们可以使用 MinHash 来实现 LSH。具体步骤如下:
- 我们将每个文本分词,并用集合来表示。例如
A = {“我”, “喜欢”, “吃”, “苹果”}, 依次推 B/C/D - 然后将所有
A~D的集合去重合并,得到一个词表如V = {“我”, “喜欢”, “吃”, “苹果”, “香蕉”, “橘子”, “不”, “水果”} - 接着为每个词表中的词分配一个编号,并按照编号顺序排列。例如
V = {0: “我”, 1: “喜欢”, 2: “吃”, 3: “苹果”, 4: “香蕉”, 5: “橘子”, 6: “不”, 7: “水果”} - 然后,我们将每个文本集合转换为一个二进制向量,其中第 i 位表示该文本是否包含第 i 个词。例如
A = [1, 1, 1, 1, 0, 0, 0, 0],D = [1, 1, 1, 0, 0, 0, 1, 1] - 接着,选择多个哈希函数,每个哈希函数都可以将二进制向量映射为一个整数。简单起见选择 3 个取余函数: (其中 x 是二进制向量的十进制表示)
h1(x) = x % 8h2(x) = (x + 1) % 8h3(x) = (x + 2) % 8
- 然后对
A~D的文本向量应用这些哈希函数,并取出最小的哈希值作为该文本的签名。例如A 的签名为[0, 1, 2],十进制为 240, h1(A) = 0,h2(A) = 1,h3(A) = 2。 - 最后,我们将每个文本的签名存储在一个哈希表中,并按照签名的值进行分桶。例如,我们可以得到以下的哈希表:
| 签名 | 文本 |
|---|---|
| [0, 1, 2] | A |
| [4, 5, 6] | B |
| [5, 6, 7] | C |
| [6, 7, 0] | D |
这样,当我们要查找与某个文本最相似的文本时,我们只需要计算出该文本对应的签名,并在对应的桶中进行比较即可。例如,如果我们要查找与 A 最相似的文本,我们只需要在签名为 [0, 1, 2] 的桶中进行比较,发现只有 A 自己,所以 A 没有相似的文本(B 同理 没有相似的文本)。
如果我们要查找与 C 最相似的文本,我们只需要在签名为 [5, 6, 7] 的桶中进行比较,发现有 C 和 D,然后计算它们之间的 Jaccard 相似度,发现 C 和 D 的相似度为 0.5,所以 C 和 D 是相似的文本。(D 和 A 同理)
LSH 只适合低维/小批量的数据, 哪怕是 128 维对它来说也会显得很高,
HNSW (图索引)
HNSW 是一篇 2016 年发表的 ANN paper, 也是目前业内 ANN 单一/组合索引中综合效果最好的之一, 首先要说明, HNSW 从定义上和聚类索引是独立/并列关系, 并不属于”图聚类“的范畴, 因为聚类的本质就是需要”分组”, 而 HNSW 是没有这一步骤的, 它核心是构建了一个带”level(层级)”的图, 然后用最短路径搜索找到最近邻居
首先回到传统的图, 一般是一个**”平面”**结构, 所有点边都在一个层级, 此时把它拓宽为多层, 也就是类似一个 graph[] 图数组, 每个图都对应为数组里的一个下标, 那么就形成了一个逻辑上的多层结构, 类似跳表 SkipList 的模式, 时间复杂度 O(logN):
HNSW 中在最高层中具有较长的边(用于快速搜索), 在较低层中具有较短的边(以便精确搜索), 简单说多层图里最顶层是入口层, 点边少, 越往下层则图越稠密, 层与层之间通过某些点来链接起来, HNSW 的实现方式和原理相对都比较复杂, 几个关键点:
- HNSW 中入口是最高层, 最为稀疏(点最少), 最底层 (L0) 最稠密,
- 在 HNSW 中, 每个向量(点)是可以存在于多个 graph level 中的, 也就是说在不同的层级都可能出现
- HNSW 的结构随着每个向量的新增而改变, 新的向量加入图时, 都会从最高层(入口)开始搜索/遍历, 逐步下降到第 0 层(底部), 它在每个层级的遍历过程中, 都会尝试连接一些最近的(邻居)点 (前提是每个点的出边 ≤ M)
同样, 为了理解我们举一个简单的例子, 假设有以下四个二维向量:A:(1,2) B:(2,3) C:(4,5) D:(5,6)
我们使用 HNSW 方式来构建一个分层的图, 并找出与给定向量最近邻的向量。可按照以下步骤进行:
- 首先,我们需要确定每个向量的层级(它在图里的最高层)。我们可以使用一个随机函数来决定,例如
l=⌊−log2u⌋,其中 u 是一个从均匀分布[0,1]中采样的随机数,l是层级。假设我们得到以下的分层结果:A: l = 0 B: l = 1 C: l = 0 D: l = 2 - 然后,我们需要确定每个向量在每一层的邻居,即与它距离最近的一些向量。这里可用一个参数
M来控制每一层的最大邻居数(假设这里设置M=2)。我们可以使用贪心/近似最近邻搜索来找到邻居。假设我们得到以下结果:- A: 第 0 层的邻居为 B 和 C
- B: 第 0 层的邻居为 A 和 C; 第 1 层的邻居为 D
- C: 第 0 层的邻居为 A 和 B
- D: 第 0 层的邻居为 B 和 C; 第 1 层的邻居为 B; 第 2 层没有邻居
- 最后,我们可以使用 HNSW 算法来查找与给定向量最近邻的向量。我们可以使用一个参数 ef 来控制搜索时的候选集大小。假设我们设置 ef=3。我们可以按照以下步骤进行:
- 假设我们要查找与向量 A 最近邻的向量。首先,我们从图中的最高层(level2)开始搜索。由于只有 D 在这一层,所以我们将 D 加入候选集,并将其作为当前节点。
- 然后,我们从当前节点的邻居中选择距离 A 最近的节点,并将其作为新的当前节点。由于 D 在第 2 层没有邻居,所以我们下降到第 1 层,并重复这一步骤。由于 D 在第 1 层只有 B 作为邻居,所以我们将 B 加入候选集,并将其作为新的当前节点。
- 接着,我们继续从当前节点的邻居中选择距离 A 最近的节点,并将其作为新的当前节点。由于 B 在第 1 层没有其他邻居,所以我们下降到第 0 层,并重复这一步骤。由于 B 在第 0 层有 A 和 C 作为邻居,所以我们将 A 和 C 加入候选集,并比较它们与 A 的距离。由于 A 自身与 A 的距离为零,所以它是最近邻节点。
- 因此,我们找到了与 A 最近邻的向量,即 A 自身。如果我们要查找与 A 次近邻的向量,我们可以从候选集中选择距离 A 第二近的向量,即 B 或 C。
Q: 在实际应用中常见的 HNSW-Flat 和 HNSW-PQ 和HNSW间是什么关系?
A: 首先 HNSW 是一个图索引的方法, Flat 则可认为是它的一个标准/原生实现方式, 存储完整的向量, 依次枚举精准搜索, 内存开销高; 而 PQ 则是一种不同的存储/搜索方式, 大幅减少时空开销的同时, 提供一个”近似的”搜索结果(准确性下降)
另外, Apache Lucene 就原生实现了 HNSW 的索引, 可以看到后面 Neo4j 就依赖它的实现进行的封装, 本质上这里 Lucene 和 Faiss的定位就比较类似, 都是一个底层库, 很多数据库可以基于它进行封装完善, 对用户提供完整的服务
(单一)索引小结
下面附一个相同 1MB 数据集下的简单对比, 来大体了解常见的向量索引方式的**”三维数据”**:
| Index | Memory (MB) | Query Time (ms) | Recall | Notes |
|---|---|---|---|---|
| Flat (L2 or IP) | ~500 | ~18 | ==1.0== | 小数据量下的最佳召回率 |
| LSH | 20 - 600 | 1.7 - 30 | 0.4 - 0.85 | 低维向量/小批量数据 |
| HNSW | 600 - 1600 | ==0.6 - 2.1== | 0.5 - 0.95 | 查询和召回效果好, 内存占用很大 |
| IVF | ~520 | 1 - 9 | 0.7 - 0.95 | 适合海量数据, 参数选择难 |
PQ (乘积量化)
PQ(Product Quantizer)是最为常见的一种(有损)压缩算法, 这里量化就是指”数据压缩”的一种方法, 方便理解你也可以叫它”乘积压缩”
它在高维向量下, 能降低高达 97%的内存占用, 以及 X5 倍 以上的搜索速度加速, 听起来似乎非常强大; 业内也有把它称之为”量化索引”, 和聚类/图/Hash 并列, 实际上感觉这个说法是不太严谨的, 容易对初学者产生误解
因为默认情况下向量都默认在内存中进行计算存储, 而大数据量下内存是有限的, PQ 就提供了一个通用的压缩算法来进行:
把每个簇中的向量, 都用中心向量来表示 (How to?), 然后维护一个所有向量到中心向量的”码本“ (what?), 大幅减少内存占用
随着维度增加, 空间中两点距离计算都会指数增长, 也就意味着高维向量需要划分相当多的”簇”, 才能有好的分类质量, 否则分类都是错的, 搜出的相似性结果也必然不准了
一个 128 维的向量, 需要维护 2^64^ 个天文大小的聚类中心才能维持较好的量化效果, 此时码本存储空间已经超过了原始分类过的向量大小
把向量分解为多个子向量, 对每个子向量进行单独的”量化“, 例如将 128 维拆成 8 * 16 维 (也就是说把长度为 128 的浮点数组拆分为 8 个子数组)
然后对 8 个子数组分别聚类, 每个 16 维的向量大概需 2^8^ = 256 (估算公式 2^(n/2)^, n 是维度), 总共仅需 8 * 256 约 2k 个聚类中心的码本即可
那么显然拆分了的向量计算之后还得合回去, 这里主要用的笛卡尔积的方式做”乘法”, 使用时合回 128 维的(近似原始)向量,
而将向量进行编码后,也将得到 8 个编码值,将它们拼起来就是该向量的最终编码值。等到使用的时候,只需要将这 8 个编码值,然后分别在 8 个子码本中搜索出对应的 16 维的向量,就能将它们使用组合成一个 128 维的向量,从而得到最终的搜索结果。
下面的动图很好的展现了这个过程: (①高维向量 -> ②均匀切分 -> ③重分配最近的中心 –> ④唯一 ID 代表对应中心值)
使用 PQ 压缩的方式,可以显著的减少内存的开销 + 加快搜索速度,弊端是搜索/召回的质量有所下降可, 可以看到它其实可应用到不同的向量索引上 (聚类/图都能使用 or 不使用这个压缩方式), 所以它并不应该和索引方式直接并列, 而应该是一个压缩选项, 否则很容易造成误解
复合索引
首先 Composite Index 对应的就是单一索引, 也就是上面提到的几个类型, 典型的聚类/图/IVF在不使用 PQ 的压缩前, 和使用后会产生巨大的差别, 所以实际应用中, 我们通常都是看到它们复合后的名词 IVF-PQ, 或者 HNSW-PQ 等单词, 实际就是复合使用索引的意思,
| 核心指标 | Flat-L2 | PQ | IVF-PQ |
|---|---|---|---|
| Recall (%) | 100 | 50 | 52 |
| Speed (ms) | 8.26 | 1.49 | 0.09 |
| Memory (MB) | 256 | 6.5 | 9.2 |
从上可以看出, IVF-PQ可以以很低的额外内存开销, 换来数量级的查询速度提升以及更好的召回率, 所以实际应用中, 复合索引几乎无处不在
Faiss (聚类库)
Faiss 全名是 Facebook AI Similarity Search, 也就是一个缩写, 之所以名气很大, 也被各类向量数据库封装使用, 在于它不仅提供了高效/可靠的相似度搜索方法, 还可处理高维向量聚类的问题。也就是说它可以看做是一个”ANN + 聚类算法的工业实现, 且支持多种距离度量方式 + 索引类型,可以根据不同的场景和需求进行选择和调整。此外, Faiss 还有 GPU 和分布式版本 (是相当完善的库实现)
- 相同之处:
- 都是基于欧氏距离的聚类算法 (即认为两个向量的距离越近,相似度越大)
- 都需要提前指定聚类的个数
K,并且使用质心作为聚类中心, 不断更新聚类中心和分配向量迭代到终止
- 不同之处:
- KMeans 是一个精确的聚类算法,即它会遍历所有的向量,计算它们到每个聚类中心的距离,并将它们分配到最近的聚类中心。这样做的优点是结果准确,缺点是时间复杂度高(尤其当向量维度和数量很大时)
- Faiss 是一个近似的聚类算法,它会使用一些加速聚类/减少开销的技巧,比如”降维/量化/倒排索引”等。这样做的优点是时间复杂度低,缺点是精准度下降(可能会产生一些误差)
聚类算法的局限性/不足:
- 最大的问题在于内存开销太大
- 多维向量用双精度浮点数表示, 也就是一个大浮点数组, 内存开销就不容小觑
- 聚类本身相当于一次”数据加工“的过程, 除了大量计算开销, 还需要单独的内存来存储每个向量的”归属“索引以及额外数据结构的空间(如树/图)
0x04. 索引类型
核心三个指标点:
- 召回率
- 查询性能
- 资源开销
基本各个模型, 都只能满足其中最多两点, 构成了不可能三角△
一般从数据结构(模型)选用上, 就至少分了 3~4 大类 (PQ 严谨说不适合作为一个单独分类):
- 图索引: 代表
HNSW以及 SSG, 是多层的立体图, 召回率高, 占用内存大, 一般适合千万级别 - 树索引: KD-Tree
- Hash/桶索引:
LSH, 百万级别内召回率能达到 100%, 但内存(空间)和计算资源(时间)消耗都大, 适合 batch 数据定向优化 - 量化索引:
PQ(一般会与其他索引复合, 常见前缀IVF-PQ), 内存占用小, 精度损失可控
目前数据量 < 千万的时候, hash/图索引的效果是最好的, 超过量级限制后, 一般采用分层的方式 (混合)
0x05. 向量数据库
这里只列举目前业内最常见的 3 种开源实现方案, 其他商业版/闭源版无法使用就暂不用调研了, 可以简单看看 Timeline 图即可:
Milvus
Milvus (/ˈmɪlvəs/)是一个 Go 实现的向量存储和检索的数据库,由国内的创业公司 Zilliz 开发(创始人叫星爵), 且于 2021 年基于 1.x 版写了一篇 paper 讲述核心内容(目前 2.x ~ 3), 作为目前开源向量数据库的头号玩家, 我们会重点关注一下它的核心特点
Qdrant
另一个强有力的开源向量数据库对手是用 Rust 编写的 Qdrant, 并且它给出了主流的 VectorDB 测评报告之一, 和 Milvus 并列为两个最出名的开源实现
PG/Redis-Vector
这种就是典型的插件式的在传统 SQL 或 NoSQL 数据库里嵌入一个向量模块, 因为本身向量数据库简单说就是提供两个功能, 一个是存储向量, 一个是计算/查找向量相似度, 前者简单说是存储一个浮点数组, 后者核心依赖的是 Faiss 或者 Apache Lucue
0x06. 与图相关
除了聚类以外,也可以通过构建树/图的方式来实现近似最近邻搜索。这种方法的基本思想是每次将向量加到数据库中的时候,就先找到与它最相邻的向量,然后将它们连接起来,这样就构成了一个图。当需要搜索的时候,就可以从图中的某个节点开始,不断的进行最相邻搜索和最短路径计算,直到找到最相似的向量。
这种算法能保证搜索的质量,但是如果图中所以的节点都以最短的路径相连,如图中最下面的一层,那么在搜索的时候,就同样需要遍历所有的节点
- Embedding 的过程三大类方案之一, 就有一个是基于图的数据结构进行的转换 (GNN:
node[vertex]2vector) - 向量数据库常见的高召回/高性能索引之一, 就是基于图的 HNSW 索引 (且目前局限在于全内存很难存下)
- KG 相关之处, 辅助 LLM 进行 prompt
0x0n. misc
- 对于传统数据库而言,1亿条数据已经是很大的业务流量。然而在向量数据库面向的场景中,单索引数据量可能达到千万/亿级别,单条向量数据的维度也会达到上千维
参考资料:
document.ai - github (VectorDB + GPT3.5 构建本地知识库)
RAG vs Finetuning — Which Is the Best Tool to Boost Your LLM Application?
作者系列